SRM 644 1 500 MakingTournament

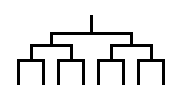
Problem Statement

It has been decided that a big tournament-style programming contest is going to take place in the wolf country! Wolf Sothe is in charge of choosing the tournament bracket.

There are N competitors, numbered 1 through N. The tournament will have exactly K rounds. In each round, some of the competitors will drop out of the tournament and some will advance. The competitors who advance from round K are the winners of the tournament. A valid tournament must have at least one winner.

Each round of the tournament must look as follows.

• At the beginning of the round, the competitors are divided into rooms. Each room must contain two or more competitors. The competitors in each room must have consecutive numbers.
• In each room the competitors compete against each other. The best competitor in each room advances and all others drop out of the tournament.
• After the round, the advancers are assigned new numbers 1 through R, where R is the number of rooms. A contestant with a smaller current number will always get a smaller new number.

For example, if there are N=6 competitors and K=2 rounds, there are 4 valid tournament brackets:


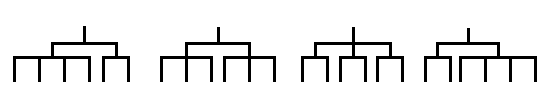
For the leftmost bracket shown above, the tournament would look as follows: In round 1 there would be two rooms: one with competitors {1,2,3,4} and the other with competitors {5,6}. After the round, the advancer from the first room would get a new number 1 and the advancer from the second room would get a new number 2. In round 2 there would be a single room containing those two competitors. The winner of that room would be the only winner of this tournament.

You are given the long N and the int K. Return the number of valid tournament brackets, modulo 1,000,000,007.

Definition

Limits

Constraints

• N will be between 1 and 1,000,000,000,000,000 (10^15), inclusive.
• K will be between 1 and 6, inclusive.

Test cases

0. input

   • N 6
   • K 2

   output

   Returns 4

   note

   Described in the statement.
1. input

   • N 8
   • K 3

   output

   Returns 1

   note

   There is only one tournament with 8 competitors and 3 rounds.
   
   
2. input

   • N 10
   • K 2

   output

   Returns 45

   note

   Note that in this test case some valid tournament brackets will have more than one winner.
3. input

   • N 63
   • K 6

   output

   Returns 0

   note

   At least 64 competitors are required to make a valid tournament bracket with 6 rounds, so the answer is 0.
4. input

   • N 1000000000000000
   • K 6

   output

   Returns 429388700